As new discoveries are constantly being made in the field of mathematics, there are still a number of unsolved problems. Many of these problems, once solved, will help to improve the quality of our daily lives.
In 2000, the Clay Mathematics Institute selected 7 different unsolved problems and offered a prize of $1 million per problem for those who find a solution. They chose to call these problems the “millennium problems”. (http://www.claymath.org/millennium/)
These problems include:
- Birch and Swinnerton-Dyer Conjecture
Ever tried to solve a quadratic equation? You just used the quadratic formula right? How about an equation of the form:y2 = x3 – x
The graph of this equation is called an elliptic curve. It turns out you can describe these curves using algebraic terms and geometric terms. The Birch Swinnerton-Dyer Conjecture says there is a connection between these two descriptions.
http://www.claymath.org/millennium/Birch_and_Swinnerton-Dyer_Conjecture/
- Hodge Conjecture
http://www.claymath.org/millennium/Hodge_Conjecture/
- Navier-Stokes Equations
http://www.claymath.org/millennium/Navier-Stokes_Equations/
- P vs NP
Ever played minesweeper? Ever wondered how fast a computer could beat the game? So do computer scientists! There are very many problems for which it is not known how fast they can be solved. The P vs NP problem seeks to show that these problems can be solved in polynomial time.
http://www.claymath.org/millennium/P_vs_NP/
- Poincaré Conjecture
Solved by Grigori Perelman in the early 21st century.
If something looks like a sphere, smells like a sphere, and tastes like a sphere, is it a sphere? In dimension two, the answer is easy. In dimensions four and greater, the answer is still yes. For a long time, the answer for dimension three was unknown until Perelman solved the problem in the early 2000’s.
http://www.claymath.org/millennium/Poincare_Conjecture/
- Riemann Hypothesis
In calculus you learn that the series
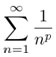
converges when p > 1. People have asked what happens when we treat p as a variable in the complex plane? It turns out this new function is related to prime numbers. The function has zeros at the negative even integers and in a small strip. Reimann’s Hypothesis is that all these extra zeros have real part equal to ½. If this is true, it implies that the primes are well spaced.
http://www.claymath.org/millennium/Riemann_Hypothesis/
- Yang-Mills Theory
http://www.claymath.org/millennium/Yang-Mills_Theory/