One day, architect Paul Stacy sat down with a pile of diamond-shaped tiles, determined to create a visual masterpiece. Called Penrose tiles, these shapes come in two sizes and two colors, but there’s more to these tiles than meets the eye.
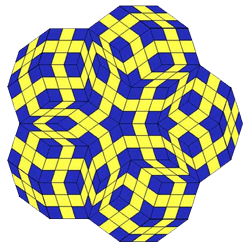
Turns out these simple diamond shapes have been the subject of mathematical theories for ages. If these tiles are assembled according to certain rules, they form a pattern that never repeats, no matter how far it’s extended. These patterns also have five-fold rotational symmetry, so the whole pattern can be turned 72 degrees and still look the same. Stacy used these tiles and their inherent mathematical properties to create a painting that was displayed at the Joint Mathematics Meetings in Washington, D.C.
Click here to see Stacy’s finished painting and to see more artwork displayed at the Joint Mathematics Meeting, including a painting based on Monge’s theorem and a sculpture inspired by a knot dipped in soapy water.